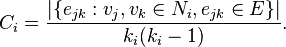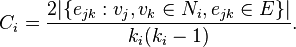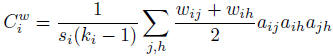Local Clustering Coefficient (LCC)
Definition
The clustering coefficient C(p) is defined as follows. Suppose that a vertex v has kv neighbours; then at most kv(kv-1)/2 edges can exist between them (this occurs when every neighbour of v is connected to every other neighbour of v). Let Cv denote the fraction of these allowable edges that actually exist. Define C as the average of Cv over all v. For friendship networks, these statistic have intuitive meanings: Cv reflects the extent to which friends of v are also friends of each other; and thus C measures the cliquishness of a typical friendship circle. [WATTS, D. 1998]
Local Clustering Coefficient
The local clustering coefficient of a vertex (node) in a graph quantifies how close its neighbors are to being a clique (complete graph).
The local clustering coefficient Ci for a vertex Vi
is then given by the proportion of links between the vertices within its
neighbourhood divided by the number of links that could possibly exist between
them.
For a directed graph, eij is distinct from eji,
and therefore for each neighbourhood Ni
there are Ki(Ki-1)
links that could exist among the vertices within the neighbourhood (Ki
is the number of neighbors of a vertex). Thus, the local clustering coefficient
for directed graphs is given as:
An undirected graph has the property that eij and eji are considered identical. Therefore, if a vertex Vi has Ki neighbours, Ki(Ki-1)/2 edges could exist among the vertices within the neighbourhood. Thus, the local clustering coefficient for undirected graphs can be defined as
Transitivity
Transitivity measures the probability that the adjacent vertices of a vertex are connected. This is sometimes also called the clustering coefficient.
The local transitivity of a vertex is the ratio of the triangles connected to the vertex and the triples centered on the vertex. For directed graph the direction of the edges is ignored.
Weighted Transitivity
There are several generalizations of transitivity to weighted graphs, and the definition by A. Barrat, is a local vertex-level quantity, its formula is
In Bipartite Networks
LIEBIG, J. & RAO, A. 2014. A Clustering Coefficient to Identify Important Nodes in Bipartite Networks. arXiv preprint arXiv:1406.5814.
Software
- GTNA
https://www.p2p.tu-darmstadt.de/research/gtna/ - Functional Genomics Assistant (FUGA)
http://code.google.com/p/fuga - JUNG
http://jung.sourceforge.net - igraph
http://igraph.org - NetworkAnalyzer
http://med.bioinf.mpi-inf.mpg.de/networkanalyzer/ - NodeXL
http://nodexl.codeplex.com/ - Pajek
http://pajek.imfm.si/ - SBEToolbox
https://github.com/biocoder/SBEToolbox/releases
References
- WATTS, D. J. & STROGATZ, S. H. 1998. Collective dynamics of 'small-world' networks. Nature, 393, 440-2.
- CSARDI, G. & NEPUSZ, T. 2006. The igraph software package for complex network research. InterJournal, Complex Systems, 1695. [http://igraph.org]
- BARRAT, A., BARTHELEMY, M., PASTOR-SATORRAS, R. & VESPIGNANI, A. 2004. The architecture of complex weighted networks. Proceedings of the National Academy of Sciences of the United States of America, 101, 3747-3752.
- JUNG, the Java Universal Network/Graph Framework [http://jung.sourceforge.net]