LeaderRank
Definition
LeaderRank is a prototype of ranking algorithms applicable to rank users in social networks.
The adaptive and parameter-free nature of LeaderRank eliminates the need of frequent calibration. LeaderRank is tolerant of spurious and missing links, which benefits applications with noisy data, especially personal relationship.
Compared with PageRank, it can find higher influential spreaders with faster convergence, and is more robust to noise and spammers.
Given a network consisting of N nodes and M directed links, a ground node connected with every node by a bidirectional link is added. Then, the network becomes strongly connected and consists of N+1 nodes and M+2N links (a bidirectional link is counted as two links with inverse directions). LeaderRank directly applies the standard random walk process to determine the score of every node. Accordingly, if the score of node i at time step t is si(t), the dynamics can be described by an iterative process as: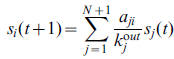 where aji is the element of the corresponding (N + 1)-dimensional adjacency
matrix, which equals 1 if there is a directed link from j to i and 0 otherwise, and
koutj is the out-degree of node j. The process starts with the initialization where
all node scores are 1 and will soon converge to a unique steady state denoted
as s∞i (i = 1, 2, · · · , N, N+1). LeaderRank ranks all nodes according to s∞i,
and the nodes with larger final scores are considered to be more influential in
spreading.
where aji is the element of the corresponding (N + 1)-dimensional adjacency
matrix, which equals 1 if there is a directed link from j to i and 0 otherwise, and
koutj is the out-degree of node j. The process starts with the initialization where
all node scores are 1 and will soon converge to a unique steady state denoted
as s∞i (i = 1, 2, · · · , N, N+1). LeaderRank ranks all nodes according to s∞i,
and the nodes with larger final scores are considered to be more influential in
spreading.
LeaderRank can also be generalized to applications ranging from blog plagiarizer identification [Gayo-Avello D, 2010], to stopping species lost in ecosystem [Allesina S, 2009]. These simple modifications may lead to substanial improvements in performance.
See also Weighted LeaderRank
The adaptive and parameter-free nature of LeaderRank eliminates the need of frequent calibration. LeaderRank is tolerant of spurious and missing links, which benefits applications with noisy data, especially personal relationship.
Compared with PageRank, it can find higher influential spreaders with faster convergence, and is more robust to noise and spammers.
Given a network consisting of N nodes and M directed links, a ground node connected with every node by a bidirectional link is added. Then, the network becomes strongly connected and consists of N+1 nodes and M+2N links (a bidirectional link is counted as two links with inverse directions). LeaderRank directly applies the standard random walk process to determine the score of every node. Accordingly, if the score of node i at time step t is si(t), the dynamics can be described by an iterative process as:
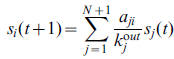
LeaderRank can also be generalized to applications ranging from blog plagiarizer identification [Gayo-Avello D, 2010], to stopping species lost in ecosystem [Allesina S, 2009]. These simple modifications may lead to substanial improvements in performance.
See also Weighted LeaderRank
Requirements
Require directed network.
Software
- From authors:
Download source code for the LeaderRank algorithm
References
- LÜ, L., ZHANG, Y.-C., YEUNG, C. H. & ZHOU, T. 2011. Leaders in Social Networks, the Delicious Case. PLoS ONE, 6, e21202.
DOI: 10.1371/journal.pone.0021202


- Gayo-Avello D (2010) Nepotistic relationships in Twitter and their impact on rank prestige algorithms. arxiv.org 1004.0816.
- Allesina S, Pascual M (2009) Googling food webs: Can an eigenvector measure species’ importance for coextinctions? PLoS Comput Bio 5: e1000494.