Flow Betweenness Centrality
Definition
Unnormalized flow betweenness
Freeman et al. define the raw or unnormalized flow betweenness of a vertex, v ∈ V(G) as: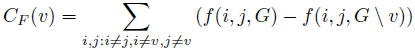
where f(i, j, G) is the maximum flow from i to j within G (under the assumption of infinite vertex
capacities, finite edge capacities, and non-simultaneity of pairwise flows). Intuitively, unnormalized
flow betweenness is simply the total maximum flow (aggregated across all pairs of third parties)
mediated by v.
Normalized flow betweenness
Normalize the raw flow betweenness by the total maximum flow among third parties (including v); this leads to the following normalized flow betweenness measure: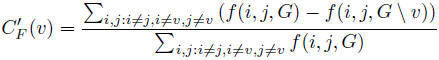
Variant by Koschutzki et al.
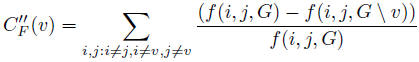where 0/0 flow ratios are treated as 0 (as in shortest-path betweenness).
Freeman et al. define the raw or unnormalized flow betweenness of a vertex, v ∈ V(G) as:
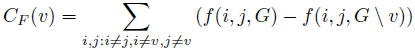
Normalized flow betweenness
Normalize the raw flow betweenness by the total maximum flow among third parties (including v); this leads to the following normalized flow betweenness measure:
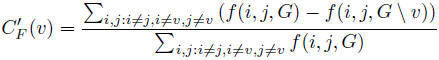
Variant by Koschutzki et al.
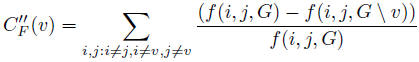
References
- FREEMAN, L. C.; BORGATTI, S.P.; and WHITE, D.R. (1991). “Centrality in Valued Graphs: A Measure of Betweenness Based on Network Flow.” Social Networks, 13(2), 141-154.
DOI: 10.1016/0378-8733(91)90017-N
- Koschutzki, D.; Lehmann, K.A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D.; Zlotowski, O. (2005). "Centrality Indices." In BRANDES, U. & ERLEBACH, T. 2005. Network Analysis: Methodological Foundations, U.S. Government Printing Office.