Entropy Centrality
Definition
Entropy centrality measures centrality of nodes depending on their contribution to the entropy of the graph.
Entropy is a fundamental concept employed in information theory and Shannon's [SHANNON, C. E. 1948] definition of entropy of a random variable X that can take n values is: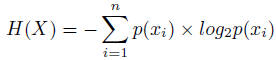
The connectivity entropy Hco and the centrality entropy measures Hce of a graph G, defined as: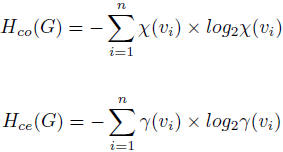
where the connectivity of a node vi ∈ V in a graph defined as χ(v) = deg(vi) / 2N where deg(vi) is the number of incident edges to node vi and N the total number of edges in the graph and
ϒ(v) = paths(vi) / paths(v1, v2, ..., vM) where paths(vi) is the number of geodesic paths from node vi to all the other nodes
in the graph and paths(v1, v2, ..., vM) is the total number of geodesic paths M that exists
across all the nodes in the graph.
The connectivity entropy measure provides information about the degree of connectivity for a node in the graph.
The centrality entropy provides information on the degree of centrality for a node in the graph. Those nodes that will split the graph in two or that will reduce substantially the number of paths available to reach other nodes when removed, will have a higher impact in decreasing the total centrality entropy of a graph.
See
Re-defined Entropy Centrality
Tutzauer, F., 2007. Entropy as a measure of centrality in networks characterized by path-transfer flow. Social networks, 29(2), pp.249-265.
Entropy is a fundamental concept employed in information theory and Shannon's [SHANNON, C. E. 1948] definition of entropy of a random variable X that can take n values is:
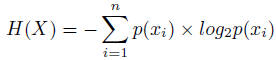
The connectivity entropy Hco and the centrality entropy measures Hce of a graph G, defined as:
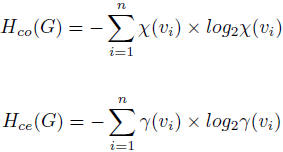
The connectivity entropy measure provides information about the degree of connectivity for a node in the graph.
The centrality entropy provides information on the degree of centrality for a node in the graph. Those nodes that will split the graph in two or that will reduce substantially the number of paths available to reach other nodes when removed, will have a higher impact in decreasing the total centrality entropy of a graph.
See
Re-defined Entropy Centrality
Tutzauer, F., 2007. Entropy as a measure of centrality in networks characterized by path-transfer flow. Social networks, 29(2), pp.249-265.
Algorithm
1: Calculate initial total entropy Hco0 (G) and Hce0 (G)
2: for all nodes 2 graph G do
3: Remove node vi, creating a modied graph G'
4: Recalculate Hcoi (G') and Hcei (G'), store these results
5: Restore original graph G
6: end for
Computational complexity
O(n^4)
References
- ORTIZ-ARROYO, D. & HUSSAIN, D. A. 2008. An information theory approach to identify sets of key players. Intelligence and Security Informatics. Springer.
- SHANNON, C. E. 1948. A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423.