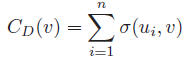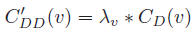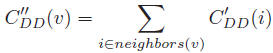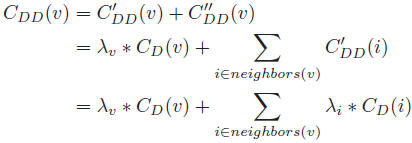Diffusion Degree

The degree centrality of node v can be defined as:

where function σ(ui, v) defined as,

σ(u_i, v) = 1 if and only if u_i and v are connected and = 0 otherwise.

In a diffusion process, a node v with propagation probability λ_v, can activate its neighbor u with probability λ_v. So, considerable contribution of node v in the diffusion process is:

When the diffusion process propagates to the next level, active neighbors of v will try to activate their inactive neighbors.Thus the cumulative contribution in the diffusion process by neighbors of v will be maximized when all of its neighbors will be activated in the previous step. In this scenario, the total contribution of neighbors of v is:

The diffusion degree of a node is defined as the cumulative contribution score of the node itself and its neighbors. So, from the above two equations we can define the diffusion degree C_DD of node v as:

• keyplayer
  https://cran.r-project.org/web/packages/keyplayer

• KUNDU, S., MURTHY, C. A. & PAL, S. K. 2011. A New Centrality Measure for Influence Maximization in Social Networks. In: KUZNETSOV, S., MANDAL, D., KUNDU, M. & PAL, S. (eds.) Pattern Recognition and Machine Intelligence. Springer Berlin Heidelberg.
• PAL, S. K., KUNDU, S. & MURTHY, C. 2014. Centrality Measures, Upper Bound, and Influence Maximization in Large Scale Directed Social Networks. Fundamenta Informaticae, 130, 317-342.