Burt's Constraint
Definition
Essentially a measure of the extent to which v is invested in people who are invested in other of v's alters (neighbors). The "constraint" is characterized by a lack of primary holes around each neighbor. Formally:
where MP(v) is the subset of v's neighbors that are both predecessors and successors of v.
Burt's constraint is higher if ego has less, or mutually stronger related (i.e. more redundant) contacts. Burt's measure of constraint, Ci, of vertex i's ego network Vi, is defined for directed and valued graphs,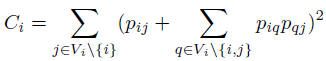
for a graph of order (ie. number of vertices) N, where proportional tie strengths are defined as:
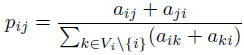ai,j are elements of A and the latter being the graph adjacency matrix. For isolated vertices, constraint is undefined.
Burt's constraint is higher if ego has less, or mutually stronger related (i.e. more redundant) contacts. Burt's measure of constraint, Ci, of vertex i's ego network Vi, is defined for directed and valued graphs,
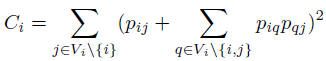
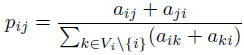
Requirements
Require directed and weigthed network.
Software
References
- BURT, R. S. 2004. Structural holes and good ideas. American journal of sociology, 110, 349-399.
- BURT, R. S. 1995. STRUCTURAL HOLES, Harvard University Press. Page 55
- CSARDI, G. & NEPUSZ, T. 2006. The igraph software package for complex network research. InterJournal, Complex Systems, 1695. [http://igraph.org]
- JUNG, the Java Universal Network/Graph Framework [http://jung.sourceforge.net]