Bridgeness Centrality
Definition
In a graph G =(V, E), where V assigns the set of nodes and E the set of links the definition of the Betweenness Centrality (BC) for a node j ∈ V stands as:
BC(j) = Bri(j) + local(j),
where
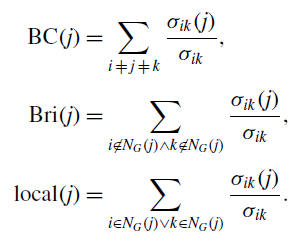Here the summation runs over any distinct node pairs i and k; σik represents the number of shortest
paths between i and k; while σik(j) is the number of such shortest paths running through j. Decomposing
BC into two parts (right-hand side) the first term defines actually the global term, bridgeness centrality,
where we consider shortest paths between nodes not in the neighbourhood of j (NG(j)), while the second
local term considers the shortest paths starting or ending in the neighbourhood of j.
where
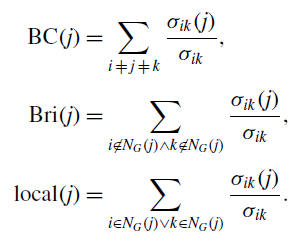
References
- Jensen, P., Morini, M., Karsai, M., Venturini, T., Vespignani, A., Jacomy, M., Cointet, J.P., Mercklé, P. and Fleury, E., 2015. Detecting global bridges in networks. Journal of Complex Networks, 4(3), pp.319-329.
DOI: 10.1093/comnet/cnv022
